
八叉树空间寻路
八叉树寻路的作用
八叉树(Octree)寻路是一种在 3D空间 中进行路径规划的技术。它的主要作用和优势包括:
1. 3D空间分割与管理
八叉树将3D空间递归地分割成8个子节点(类似于2D中的四叉树)
可以高效地表示复杂的3D环境,包括有高度差异的地形
2. 主要应用场景
3. 相比2D寻路的优势
传统2D寻路(NavMesh/Grid):只考虑水平面移动
八叉树3D寻路:支持上下左右前后全方位移动4. 空间优化
稀疏表示:空旷区域用大节点表示,复杂区域细分为小节点
动态更新:可以高效地更新局部空间变化
内存高效:只存储必要的空间信息
5. 与A算法结合 八叉树通常与A等寻路算法结合使用: - 八叉树节点作为寻路图的节点 - 相邻节点之间建立连接 - 使用启发式搜索找到最优路径
简单示意
┌───────────┐
│ 根节点 │ (整个3D空间)
└─────┬─────┘
│
┌────┬───┴───┬────┐
↓ ↓ ↓ ↓
┌──┐ ┌──┐ ┌──┐ ┌──┐ × 8个子节点
└──┘ └──┘ └──┘ └──┘
↓
继续细分...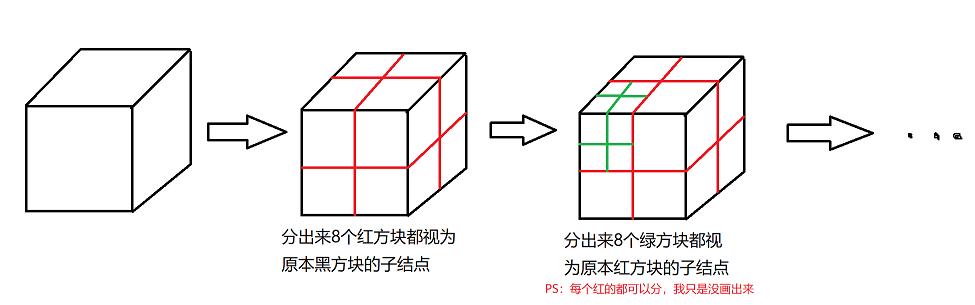
开始创建八叉树
1. 创建节点
子节点方块的布置如下图所示
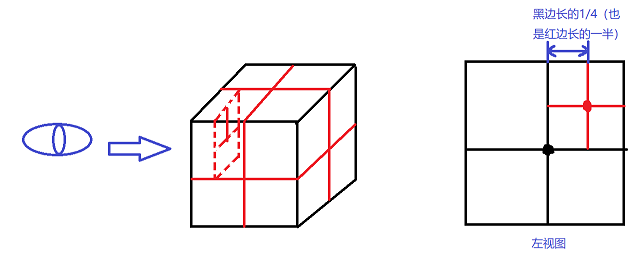
简单分析可知, 每个子节点中心的位置都是从父节点中心偏移 四分之一 父节点边长 而来
而且偏移的方向都是在 X, Y, Z 三条轴上,8个子节点对应了8种偏移位置
所以我们可以用1-8的二进制来表示这三个位置(000, 001, 010, 011, 100, 101, 110, 111)
用每个位置上的 0 来区分 X, Y, Z 上偏移的方向
对应代码如下:
using System.Collections.Generic;
using UnityEngine;
public class OctreeTreeNode
{
/// <summary>
/// 分割单元最小尺寸
/// </summary>
private readonly float MIN_SIZE = 1.0f;
/// <summary>
/// 父节点
/// </summary>
public OctreeTreeNode parent { get; private set; }
/// <summary>
/// 子节点列表
/// </summary>
public List<OctreeTreeNode> child;
/// <summary>
/// 包围盒作为节点方块
/// </summary>
public Bounds nodeCube { get; private set; }
public OctreeTreeNode(OctreeTreeNode parent, Bounds nodeCube)
{
this.parent = parent;
this.nodeCube = nodeCube;
}
public void Divide()
{
if (nodeCube.size.x / 2 < MIN_SIZE)
{
return;
}
float childHalfSize = nodeCube.size.x / 4;
if (child == null)
{
child = new List<OctreeTreeNode>();
}
Vector3 offest; // 子节点相对于父节点的偏移量
for (int i = 0; i < 8; i++)
{
offest = new Vector3(
((i & 1) == 0) ? -childHalfSize : childHalfSize, // 001
((i & 2) == 0) ? -childHalfSize : childHalfSize, // 010
((i & 4) == 0) ? -childHalfSize : childHalfSize // 100
);
Bounds childBounds = new Bounds(
nodeCube.center + offest,
new Vector3(childHalfSize * 2, childHalfSize * 2, childHalfSize * 2)
);
OctreeTreeNode childNode = new OctreeTreeNode(this, childBounds);
child.Add(childNode);
childNode.Divide();
}
}
}为了方便观察结果,在类中添个用于绘制方块的函数,当它在OnDrawGizmos中调用时就可以看到方块了
public void Draw(bool isSeeOne)
{
Gizmos.color = Color.green;
Gizmos.DrawWireCube(NodeCube.center, NodeCube.size);
if (Children == null)
return;
foreach(var c in Children)
{
c.Draw(isSeeOne);
if(isSeeOne)
{
break;
}
}
}为了方便在Unity中使用,我们创建一个继承了 MonoBehaviour 的类 CreatOctreeTree,并将它挂在一个边长为8的Cube上:
public class CreatOctreeTree : MonoBehaviour
{
public bool isSeeOne = true; //只看分裂后的一个
private OctreeTreeNode node;
private void Awake()
{
//用Cube本身的包围盒做为起始尺寸进行划分
node = new OctreeTreeNode(node, GetComponent<Renderer>().bounds);
node.Divide();
}
private void OnDrawGizmos()
{
if (Application.isPlaying)
{
node.Draw(isSeeOne);
}
}
}
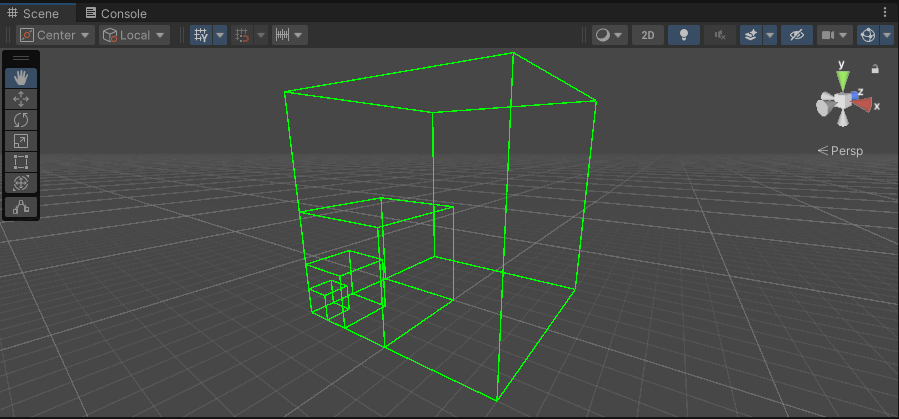
运行查看, 我们创建了一个边长为 8 的 Cube, 一共分裂了 3 次, 符合预期
创建节点完整代码
using System.Collections.Generic;
using UnityEngine;
public class OctreeTreeNode
{
/// <summary>
/// 分割单元最小尺寸
/// </summary>
private readonly float MIN_SIZE = 1.0f;
/// <summary>
/// 父节点
/// </summary>
public OctreeTreeNode parent { get; private set; }
/// <summary>
/// 子节点列表
/// </summary>
public List<OctreeTreeNode> child;
/// <summary>
/// 包围盒作为节点方块
/// </summary>
public Bounds nodeCube { get; private set; }
public OctreeTreeNode(OctreeTreeNode parent, Bounds nodeCube)
{
this.parent = parent;
this.nodeCube = nodeCube;
}
public void Divide()
{
if (nodeCube.size.x / 2 < MIN_SIZE)
{
return;
}
float childHalfSize = nodeCube.size.x / 4;
if (child == null)
{
child = new List<OctreeTreeNode>();
}
Vector3 offest; // 子节点相对于父节点的偏移量
for (int i = 0; i < 8; i++)
{
offest = new Vector3(
((i & 1) == 0) ? -childHalfSize : childHalfSize, // 001
((i & 2) == 0) ? -childHalfSize : childHalfSize, // 010
((i & 4) == 0) ? -childHalfSize : childHalfSize // 100
);
Bounds childBounds = new Bounds(
nodeCube.center + offest,
new Vector3(childHalfSize * 2, childHalfSize * 2, childHalfSize * 2)
);
OctreeTreeNode childNode = new OctreeTreeNode(this, childBounds);
child.Add(childNode);
childNode.Divide();
}
}
//isSeeOne为true,则只查看分裂后的一个,否则查看所有分裂后的方块
public void Draw(bool isSeeOne)
{
Gizmos.color = Color.green;
Gizmos.DrawWireCube(nodeCube.center, nodeCube.size);
if (child == null)
return;
foreach (var c in child)
{
c.Draw(isSeeOne);
if (isSeeOne)
{
break;
}
}
}
}
public class CreatOctreeTree : MonoBehaviour
{
public bool isSeeOne = true; //只看分裂后的一个
private OctreeTreeNode node;
private void Awake()
{
//用Cube本身的包围盒做为起始尺寸进行划分
node = new OctreeTreeNode(node, GetComponent<Renderer>().bounds);
node.Divide();
}
private void OnDrawGizmos()
{
if (Application.isPlaying)
{
node.Draw(isSeeOne);
}
}
}
2. 寻找根节点
游戏场景往往是多变的,一直用一个Cube去试显然不是高效的方案。
Unity内置了一个方法可以为我们解决这个问题

Encapsulate 方法可以让包围盒自行扩大以容纳下传进来的包围盒。所以我们让一个包围盒把场景中的所有物体都容纳进去,这样就能得到足够大的包围盒了。我们新建一个MyOctree类:
public class MyOctreetree
{
public OctreeTreeNode rootNode { get; private set; }
public MyOctreetree(List<GameObject> objects)
{
if (objects == null || objects.Count == 0)
return;
// 用第一个物体的包围盒初始化
var baseCube = objects[0].GetComponent<Renderer>().bounds;
// 将剩余对象的包围盒合并
for (int i = 1; i < objects.Count; i++)
{
baseCube.Encapsulate(objects[i].GetComponent<Renderer>().bounds);
}
// 将包围盒调整为立方体
var cubeSize = Mathf.Max(baseCube.size.x, Mathf.Max(baseCube.size.y, baseCube.size.z)) * Vector3.one;
baseCube.SetMinMax(baseCube.center - cubeSize / 2f, baseCube.center + cubeSize / 2f);
rootNode = new OctreeTreeNode(null, baseCube);
rootNode.Divide();
}
}注意baseCube的bounds只能用用第一个物体的包围盒初始化,不能直接 new() ,因为当你使用 new Bounds() 创建一个空的包围盒时,它的 center 是 (0,0,0),size 是 (0,0,0)。
当你调用 Encapsulate 时,它会扩展包围盒以同时包含原点 (0,0,0) 和物体的包围盒,导致最终的 baseCube 包含了从原点到物体位置的整个区域。
顺便也改改 CreatOctreeTree 脚本,让它画出八叉树,而不是单一节点:
public class CreatOctreeTree : MonoBehaviour
{
/// <summary>
/// 只看分裂后的一个
/// </summary>
public bool isSeeOne = true;
/// <summary>
/// 需要划分八叉树的物体列表
/// </summary>
public List<GameObject> objects;
/// <summary>
/// 八叉树
/// </summary>
private MyOctreetree myOctreetree;
private void Awake()
{
// 获取场景中有 Render 的 GameObject
var renderers = FindObjectsOfType<Renderer>();
objects = new List<GameObject>();
foreach (var renderer in renderers)
{
objects.Add(renderer.gameObject);
}
myOctreetree = new MyOctreetree(objects);
}
private void OnDrawGizmos()
{
if (Application.isPlaying)
{
myOctreetree.rootNode.Draw(isSeeOne);
}
}
}随便在场景里摆了几个立方体,最终生成的最大包围盒能将它们都裹住:
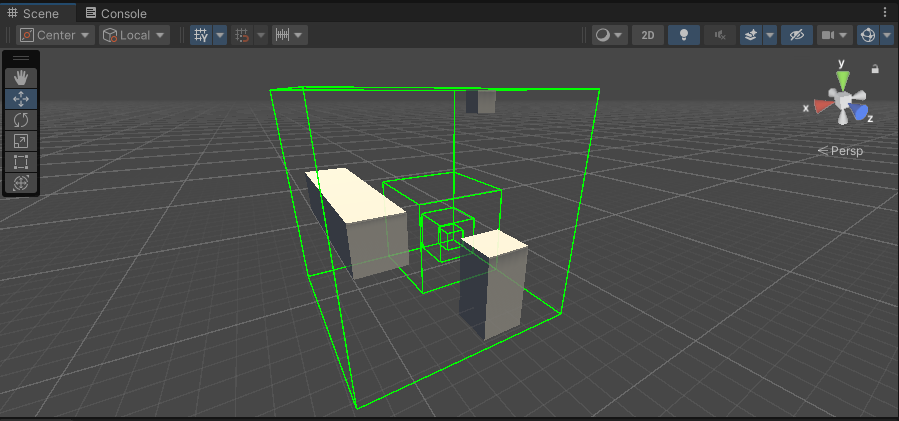
但是现在有一个问题,当场景变大包围盒跟着变大时,我们需要分割的次数也会跟着上升,我们使用的Divide函数为递归调用,每递归深度加一都要进行8n次方次分割,这会带来巨大的性能开销,因此我们要进行一些优化。
3. 性能优化
Ⅰ. 限制递归深度
首先最容易想到的就是限制递归深度
我们为代码添加最大递归深度,并实时追踪当前深度,当递归达到最大深度时退出分割递归。
using System.Collections.Generic;
using UnityEngine;
public class OctreeTreeNode
{
/// <summary>
/// 分割单元最小尺寸
/// </summary>
private float minSize;
/// <summary>
/// 最大递归深度
/// </summary>
private int maxDepth;
/// <summary>
/// 当前节点深度
/// </summary>
private int depth;
/// <summary>
/// 父节点
/// </summary>
public OctreeTreeNode parent { get; private set; }
/// <summary>
/// 子节点列表
/// </summary>
public List<OctreeTreeNode> child;
/// <summary>
/// 包围盒作为节点方块
/// </summary>
public Bounds nodeCube { get; private set; }
public OctreeTreeNode(OctreeTreeNode parent, Bounds nodeCube, int depth, float minSize, int maxDepth)
{
this.parent = parent;
this.nodeCube = nodeCube;
this.depth = depth;
this.minSize = minSize;
this.maxDepth = maxDepth;
}
public void Divide()
{
if (nodeCube.size.x / 2 < minSize || depth >= maxDepth)
{
return;
}
float childHalfSize = nodeCube.size.x / 4;
if (child == null)
{
child = new List<OctreeTreeNode>();
}
Vector3 offest; // 子节点相对于父节点的偏移量
for (int i = 0; i < 8; i++)
{
offest = new Vector3(
((i & 1) == 0) ? -childHalfSize : childHalfSize, // 001
((i & 2) == 0) ? -childHalfSize : childHalfSize, // 010
((i & 4) == 0) ? -childHalfSize : childHalfSize // 100
);
Bounds childBounds = new Bounds(
nodeCube.center + offest,
new Vector3(childHalfSize * 2, childHalfSize * 2, childHalfSize * 2)
);
OctreeTreeNode childNode = new OctreeTreeNode(this, childBounds, depth + 1, minSize, maxDepth);
child.Add(childNode);
childNode.Divide();
}
}
//isSeeOne为true,则只查看分裂后的一个,否则查看所有分裂后的方块
public void Draw(bool isSeeOne)
{
Gizmos.color = Color.green;
Gizmos.DrawWireCube(nodeCube.center, nodeCube.size);
if (child == null)
return;
foreach (var c in child)
{
c.Draw(isSeeOne);
if (isSeeOne)
{
break;
}
}
}
}
public class MyOctreetree
{
public OctreeTreeNode rootNode { get; private set; }
public MyOctreetree(List<GameObject> objects, float minSize, int maxDepth)
{
if (objects == null || objects.Count == 0)
return;
// 用第一个物体的包围盒初始化
var baseCube = objects[0].GetComponent<Renderer>().bounds;
// 将剩余对象的包围盒合并
for (int i = 1; i < objects.Count; i++)
{
baseCube.Encapsulate(objects[i].GetComponent<Renderer>().bounds);
}
// 将包围盒调整为立方体
var cubeSize = Mathf.Max(baseCube.size.x, Mathf.Max(baseCube.size.y, baseCube.size.z)) * Vector3.one;
baseCube.SetMinMax(baseCube.center - cubeSize / 2f, baseCube.center + cubeSize / 2f);
rootNode = new OctreeTreeNode(null, baseCube, 0, minSize, maxDepth);
rootNode.Divide();
}
}
public class CreatOctreeTree : MonoBehaviour
{
/// <summary>
/// 只看分裂后的一个
/// </summary>
public bool isSeeOne = true;
/// <summary>
/// 分割单元最小尺寸
/// </summary>
[Range(0.1f, 10f)]
public float minSize = 1.0f;
/// <summary>
/// 最大递归深度
/// </summary>
[Range(1, 10)]
public int maxDepth = 5;
/// <summary>
/// 需要划分八叉树的物体列表
/// </summary>
public List<GameObject> objects;
/// <summary>
/// 八叉树
/// </summary>
private MyOctreetree myOctreetree;
/// <summary>
/// 八叉树构建时间(毫秒)
/// </summary>
[Header("构建信息")]
public float buildTimeMs;
private void Awake()
{
// 获取场景中有Render的GameObject
var renderers = FindObjectsOfType<Renderer>();
objects = new List<GameObject>();
foreach (var renderer in renderers)
{
objects.Add(renderer.gameObject);
}
var stopwatch = System.Diagnostics.Stopwatch.StartNew();
myOctreetree = new MyOctreetree(objects, minSize, maxDepth);
stopwatch.Stop();
buildTimeMs = stopwatch.ElapsedMilliseconds;
Debug.Log($"八叉树构建完成,耗时: {buildTimeMs} ms");
}
private void OnDrawGizmos()
{
if (Application.isPlaying)
{
myOctreetree.rootNode.Draw(isSeeOne);
}
}
}
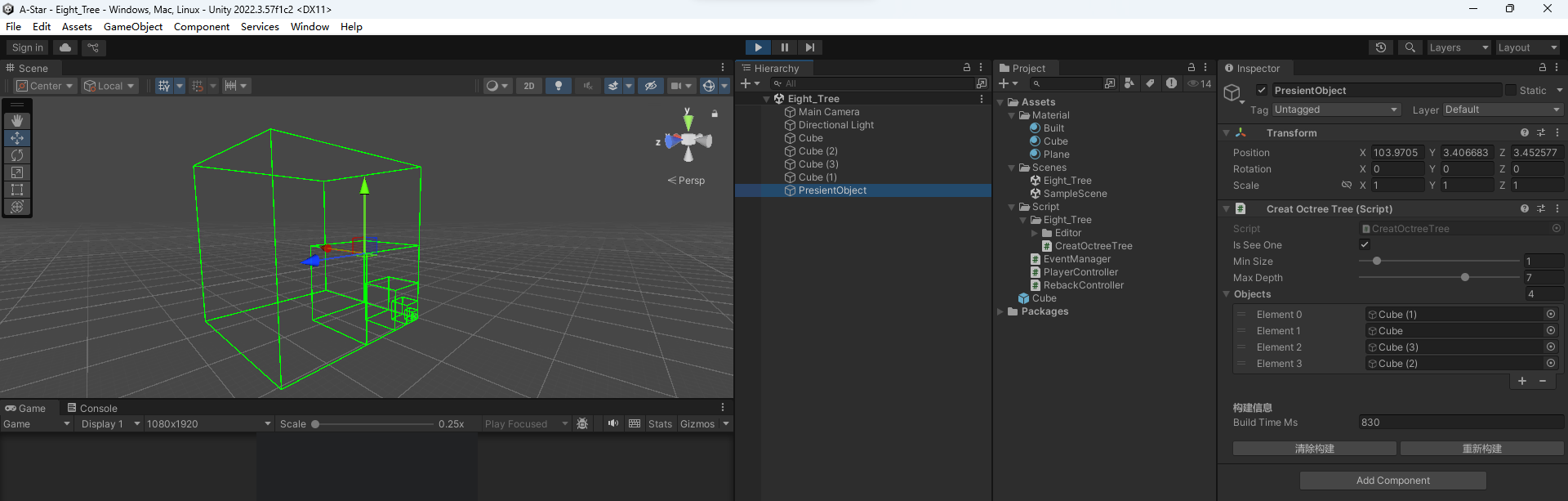
递归深度为 7 时,耗时 830 ms
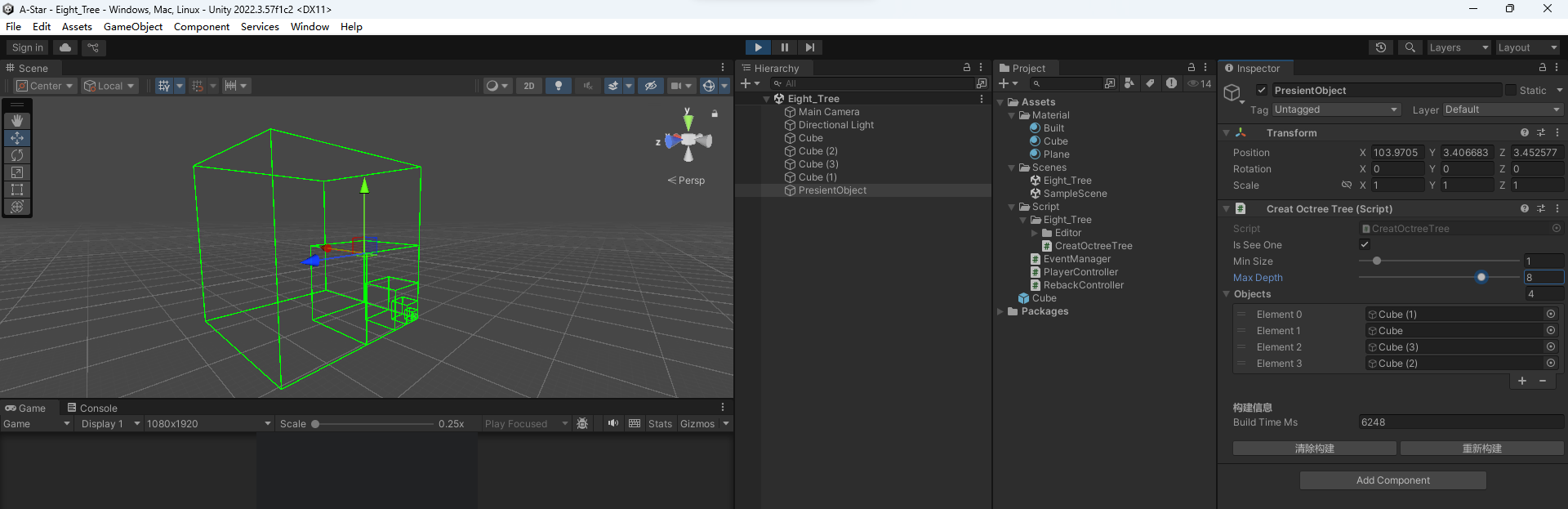
递归深度为 8 时,耗时 6248 ms
可以看到限制了递归深度后,构建耗时明显下降
但仅仅限制递归深度并不完善而且当物体体积较小时精度并不准确
所以我们还需要一种更有策略性的优化方式 —— 前剪枝
Ⅱ. 前剪枝
什么是前剪枝?
前剪枝(Pre-pruning)
是决策树和八叉树等树形数据结构中的一种优化策略。
定义:在树的构建过程中,提前停止节点的分裂,而不是等树完全构建后再进行修剪。
在我们的代码中,对递归深度进行限制也是一种前剪枝策略
现在我将说明一种更具有针对性的前剪枝策略
我们可以注意到,其实有一些方块没必要继续分裂下去。分裂行为其实是有目的的:检测出哪里有障碍物。一个大方块不断分裂变小,就是更进一步定位内部障碍物位置的过程,如果它一开始就没碰到什么障碍物,那也没必要分裂了。
在 MyOctreetree 中将第一个包围盒中的所有Collider收集起来,传入到rootNode的分割当中
public class MyOctreetree
{
public OctreeTreeNode rootNode { get; private set; }
public MyOctreetree(List<GameObject> objects, float minSize, int maxDepth)
{
if (objects == null || objects.Count == 0)
return;
// 用第一个物体的包围盒初始化
var baseCube = objects[0].GetComponent<Renderer>().bounds;
// 将剩余对象的包围盒合并
for (int i = 1; i < objects.Count; i++)
{
baseCube.Encapsulate(objects[i].GetComponent<Renderer>().bounds);
}
// 将包围盒调整为立方体
var cubeSize = Mathf.Max(baseCube.size.x, Mathf.Max(baseCube.size.y, baseCube.size.z)) * Vector3.one;
baseCube.SetMinMax(baseCube.center - cubeSize / 2f, baseCube.center + cubeSize / 2f);
rootNode = new OctreeTreeNode(null, baseCube, 0, minSize, maxDepth);
var colliders = new List<Collider>();
foreach (var o in objects)
{
if (o.TryGetComponent<Collider>(out var collider))
{
colliders.Add(collider);
}
}
rootNode.Divide(colliders);
}
}在 Divide 中,我们先判断当前节点是否与之前收集的Collider有相交,若没有相交,则该节点不再进行分割
public void Divide(List<Collider> colliders)
{
if (nodeCube.size.x / 2 < minSize || depth >= maxDepth)
{
return;
}
// 找出与当前节点包围盒相交的碰撞体
var intersecting = colliders.FindAll(c => nodeCube.Intersects(c.bounds));
// 前剪枝:没有物体相交则停止
if (intersecting.Count == 0)
{
return;
}
float childHalfSize = nodeCube.size.x / 4;
if (child == null)
{
child = new List<OctreeTreeNode>();
}
Vector3 offest; // 子节点相对于父节点的偏移量
for (int i = 0; i < 8; i++)
{
offest = new Vector3(
((i & 1) == 0) ? -childHalfSize : childHalfSize, // 001
((i & 2) == 0) ? -childHalfSize : childHalfSize, // 010
((i & 4) == 0) ? -childHalfSize : childHalfSize // 100
);
Bounds childBounds = new Bounds(
nodeCube.center + offest,
new Vector3(childHalfSize * 2, childHalfSize * 2, childHalfSize * 2)
);
OctreeTreeNode childNode = new OctreeTreeNode(this, childBounds, depth + 1, minSize, maxDepth);
child.Add(childNode);
childNode.Divide(intersecting); // 只传递相交的碰撞体
}
}我们来看一下进行了前剪枝后的性能
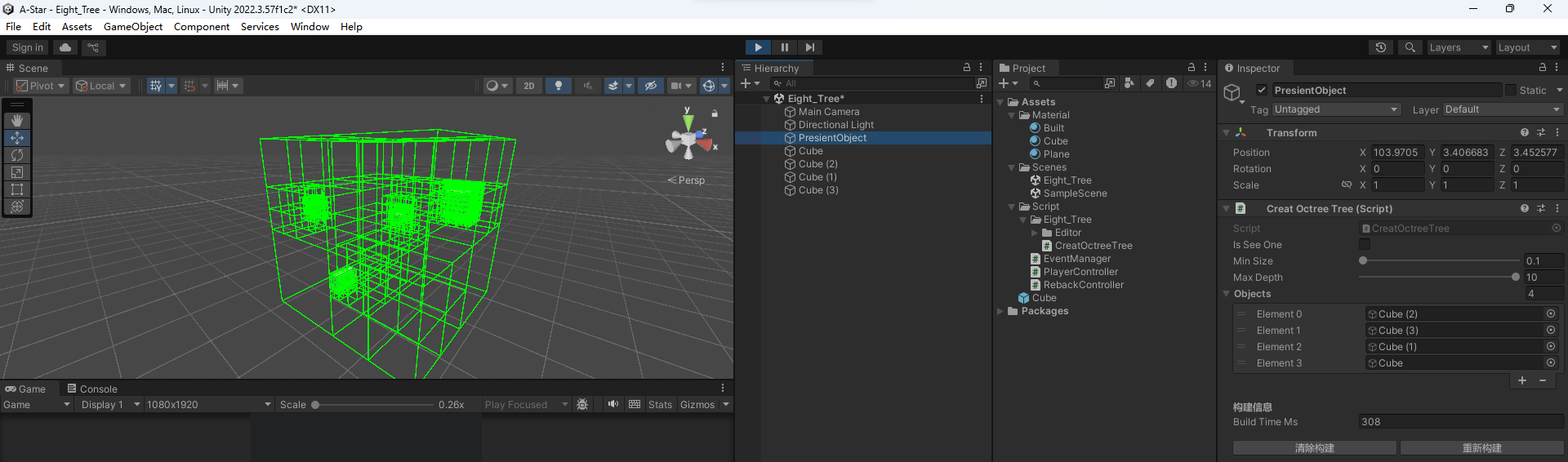
调大了递归深度,减小了最小分割长度,构建速度依旧远超之前 !!!
至此我们就创建好了八叉树,并得到了每一个节点。
4. 连接网格
Ⅰ. 收集节点
通过观察我们知道,每一个节点都为一个正方体,有六个面,所以我们可以一个节点与相邻的六个节点连接起来,我们称为 邻居连接
同时我们要剔除包含了障碍物的节点
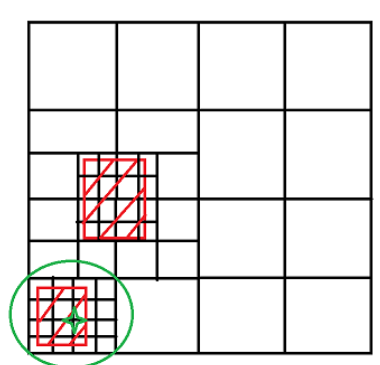
通过这个图我们很容易可以看出包含障碍物的节点一定是不能再分割的节点(叶子节点)
什么情况不能再分割
节点不包含障碍物
节点包含障碍物,但是已经到达分割最小单元或最大递归深度
显然符合我们需求的是第二种
if (nodeCube.size.x / 2 < minSize || depth >= maxDepth)
{
// 叶子节点:检查是否与障碍物相交
isBlocked = colliders.Exists(c => nodeCube.Intersects(c.bounds));
return;
}所以我们直接在进入最小分割单元或最大递归深度里判断该节点是否包含障碍物即可得到障碍物节点
在 OctreeTreeNode 中添加用于邻居连接的字段
/// <summary>
/// 是否包含障碍物(与碰撞体相交)
/// </summary>
public bool isBlocked = false;
/// <summary>
/// 所有共享面邻居节点列表
/// </summary>
public List<OctreeTreeNode> neighbors = new List<OctreeTreeNode>();
/// <summary>
/// 获取包围盒的最小点
/// </summary>
public Vector3 Min => nodeCube.min;
/// <summary>
/// 获取包围盒的最大点
/// </summary>
public Vector3 Max => nodeCube.max;
/// <summary>
/// 判断是否为叶子节点
/// </summary>
public bool IsLeaf => child == null || child.Count == 0;
/// <summary>
/// 是否可通行(叶子节点且不包含障碍物)
/// </summary>
public bool IsWalkable => IsLeaf && !isBlocked;在 MyOctreetree 中添加储存叶子节点的列表,以及收集叶子列表的方法
/// <summary>
/// 叶子节点列表
/// </summary>
public List<OctreeTreeNode> leafNodes { get; private set; }
/// <summary>
/// 递归收集所有叶子节点
/// </summary>
private void CollectLeafNodes(OctreeTreeNode node)
{
if (node == null) return;
// 只收集不含障碍物的叶子节点
if (node.IsLeaf)
{
if (node.isBlocked)
{
return;
}
leafNodes.Add(node);
return;
}
// 非叶子节点,递归处理子节点
foreach (var c in node.child)
{
CollectLeafNodes(c);
}
}Ⅱ. 建立邻居连接
建立连接条件
1.两个节点有共享面
判断“是否共享面”
两个叶节点 A / B:
A.max.x == B.min.x 或反过来
且 Y、Z 区间有重叠
共享面 =
|Axmax - Bxmin| < ε
AND overlap(A.y, B.y)
AND overlap(A.z, B.z)
区间重叠
情况1: 有重叠
区间A: |---------|
aMin aMax
区间B: |---------|
bMin bMax
重叠: |-----|
overlapMin overlapMax
(=bMin) (=aMax)
情况2: 无重叠
区间A: |-----|
aMax
区间B: |-----|
bMin
此时 overlapMin(bMin) > overlapMax(aMax)
结果为负数 → 返回02.共享面的面积大于阈值
这一步能直接避免:
AI 卡边
穿过“细缝”
数值抖动
接下来在 MyOctreetree 中添加字段和为叶子节点建立邻居连接的方法
/// <summary>
/// 共享面最小面积阈值(小于此值不建立连接)
/// </summary>
private float minSharedAreaThreshold;
/// <summary>
/// 浮点数比较容差
/// </summary>
private const float EPSILON = 0.001f;
/// <summary>
/// 基于共享面为叶子节点建立邻居连接
/// 使用双重循环遍历所有叶子节点对,检测共享面
/// </summary>
private void BuildNeighborConnectionsBySharedFace()
{
int count = leafNodes.Count;
for (int i = 0; i < count; i++)
{
for (int j = i + 1; j < count; j++)
{
var nodeA = leafNodes[i];
var nodeB = leafNodes[j];
// 检测是否有共享面
if (HasSharedFace(nodeA, nodeB, out float sharedArea))
{
// 面积大于阈值才建立连接
if (sharedArea >= minSharedAreaThreshold)
{
// 双向连接
nodeA.neighbors.Add(nodeB);
nodeB.neighbors.Add(nodeA);
}
}
}
}
}
/// <summary>
/// 检测两个节点是否有共享面
/// </summary>
/// <param name="a">节点A</param>
/// <param name="b">节点B</param>
/// <param name="sharedArea">输出共享面积</param>
/// <returns>是否有共享面</returns>
private bool HasSharedFace(OctreeTreeNode a, OctreeTreeNode b, out float sharedArea)
{
sharedArea = 0f;
// 检查X轴方向的共享面 (A.max.x == B.min.x 或 A.min.x == B.max.x)
if (Mathf.Abs(a.Max.x - b.Min.x) < EPSILON || Mathf.Abs(a.Min.x - b.Max.x) < EPSILON)
{
// 计算Y和Z的重叠区间
float overlapY = CalculateOverlap(a.Min.y, a.Max.y, b.Min.y, b.Max.y);
float overlapZ = CalculateOverlap(a.Min.z, a.Max.z, b.Min.z, b.Max.z);
if (overlapY > 0 && overlapZ > 0)
{
sharedArea = overlapY * overlapZ;
return true;
}
}
// 检查Y轴方向的共享面 (A.max.y == B.min.y 或 A.min.y == B.max.y)
if (Mathf.Abs(a.Max.y - b.Min.y) < EPSILON || Mathf.Abs(a.Min.y - b.Max.y) < EPSILON)
{
// 计算X和Z的重叠区间
float overlapX = CalculateOverlap(a.Min.x, a.Max.x, b.Min.x, b.Max.x);
float overlapZ = CalculateOverlap(a.Min.z, a.Max.z, b.Min.z, b.Max.z);
if (overlapX > 0 && overlapZ > 0)
{
sharedArea = overlapX * overlapZ;
return true;
}
}
// 检查Z轴方向的共享面 (A.max.z == B.min.z 或 A.min.z == B.max.z)
if (Mathf.Abs(a.Max.z - b.Min.z) < EPSILON || Mathf.Abs(a.Min.z - b.Max.z) < EPSILON)
{
// 计算X和Y的重叠区间
float overlapX = CalculateOverlap(a.Min.x, a.Max.x, b.Min.x, b.Max.x);
float overlapY = CalculateOverlap(a.Min.y, a.Max.y, b.Min.y, b.Max.y);
if (overlapX > 0 && overlapY > 0)
{
sharedArea = overlapX * overlapY;
return true;
}
}
return false;
}
/// <summary>
/// 计算两个一维区间的重叠长度
/// </summary>
/// <param name="aMin">区间A最小值</param>
/// <param name="aMax">区间A最大值</param>
/// <param name="bMin">区间B最小值</param>
/// <param name="bMax">区间B最大值</param>
/// <returns>重叠长度,无重叠返回0</returns>
private float CalculateOverlap(float aMin, float aMax, float bMin, float bMax)
{
float overlapMin = Mathf.Max(aMin, bMin);
float overlapMax = Mathf.Min(aMax, bMax);
return Mathf.Max(0, overlapMax - overlapMin);
}更新 MyOctreetree 构造方法
public MyOctreetree(List<GameObject> objects, float minSize, int maxDepth, float minSharedArea = 0.01f)
{
if (objects == null || objects.Count == 0)
return;
// 用第一个物体的包围盒初始化
var baseCube = objects[0].GetComponent<Renderer>().bounds;
// 将剩余对象的包围盒合并
for (int i = 1; i < objects.Count; i++)
{
baseCube.Encapsulate(objects[i].GetComponent<Renderer>().bounds);
}
// 将包围盒调整为立方体
var cubeSize = Mathf.Max(baseCube.size.x, Mathf.Max(baseCube.size.y, baseCube.size.z)) * Vector3.one;
baseCube.SetMinMax(baseCube.center - cubeSize / 2f, baseCube.center + cubeSize / 2f);
rootNode = new OctreeTreeNode(null, baseCube, 0, minSize, maxDepth);
var colliders = new List<Collider>();
foreach (var o in objects)
{
if (o.TryGetComponent<Collider>(out var collider))
{
colliders.Add(collider);
}
}
rootNode.Divide(colliders);
// 收集叶子节点
leafNodes = new List<OctreeTreeNode>();
CollectLeafNodes(rootNode);
// 设置最小共享面积阈值
minSharedAreaThreshold = minSharedArea;
// 基于共享面为可通行节点建立邻居连接
BuildNeighborConnectionsBySharedFace();
}更新 OctreeTreeNode 中的 Draw 方法, 将连接线绘制出来
//isSeeOne为true,则只查看分裂后的一个,否则查看所有分裂后的方块
public void Draw(bool isSeeOne, bool drawConnections = false, bool drawBounds = true)
{
// 根据是否包含障碍物设置颜色
if (drawBounds)
{
if (IsLeaf)
{
Gizmos.color = isBlocked ? Color.red : Color.green;
}
else
{
Gizmos.color = Color.white;
}
Gizmos.DrawWireCube(nodeCube.center, nodeCube.size);
}
// 绘制邻居连接线(只绘制可通行节点的连接)
if (drawConnections && IsWalkable)
{
Gizmos.color = Color.yellow;
foreach (var neighbor in neighbors)
{
// 只绘制一半的连接线,避免重复绘制
if (neighbor != null && neighbor.GetHashCode() > this.GetHashCode())
{
Gizmos.DrawLine(nodeCube.center, neighbor.nodeCube.center);
}
}
}
if (child == null)
return;
foreach (var c in child)
{
c.Draw(isSeeOne, drawConnections, drawBounds);
if (isSeeOne)
{
break;
}
}
}最后连接效果
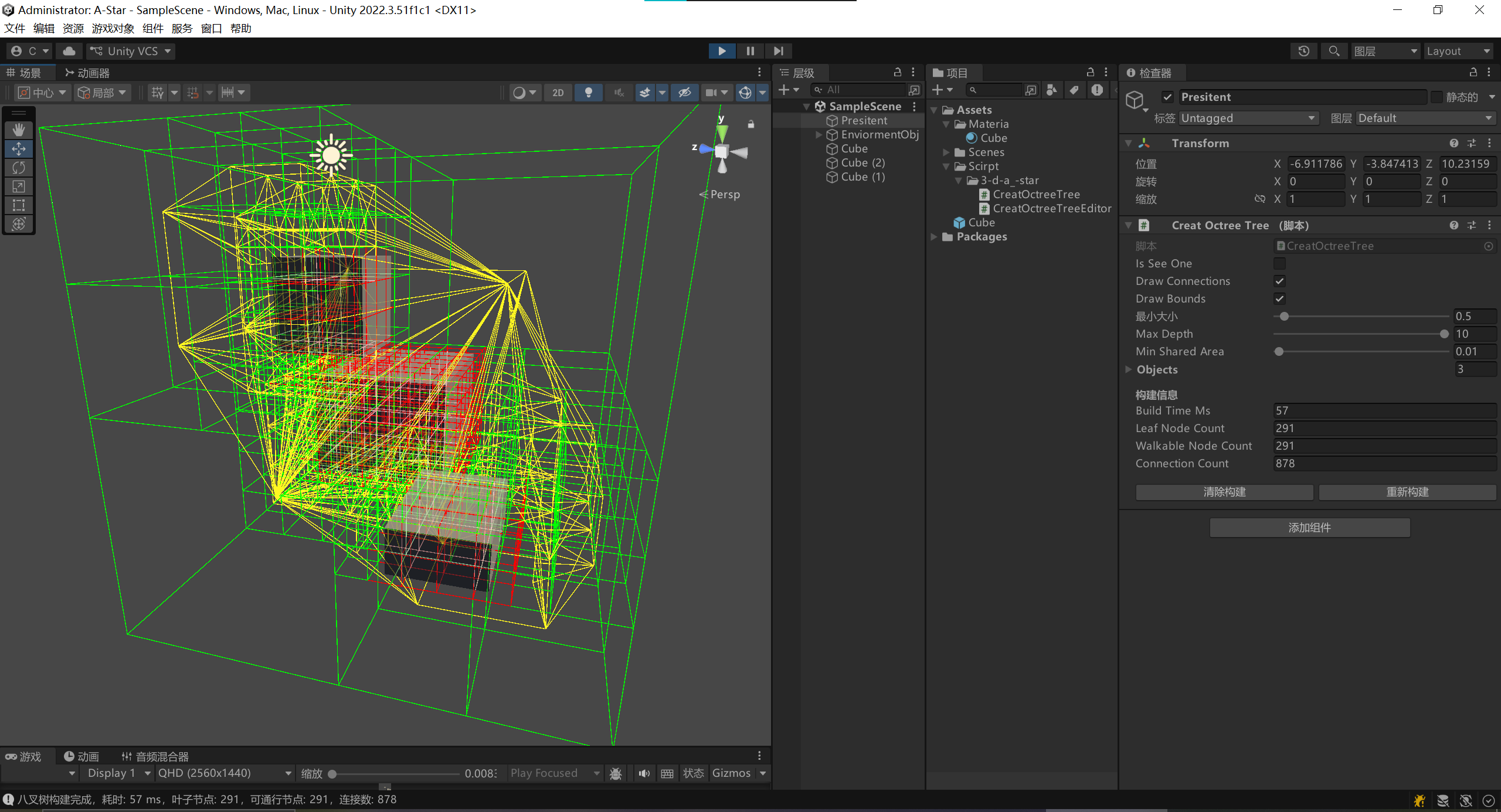
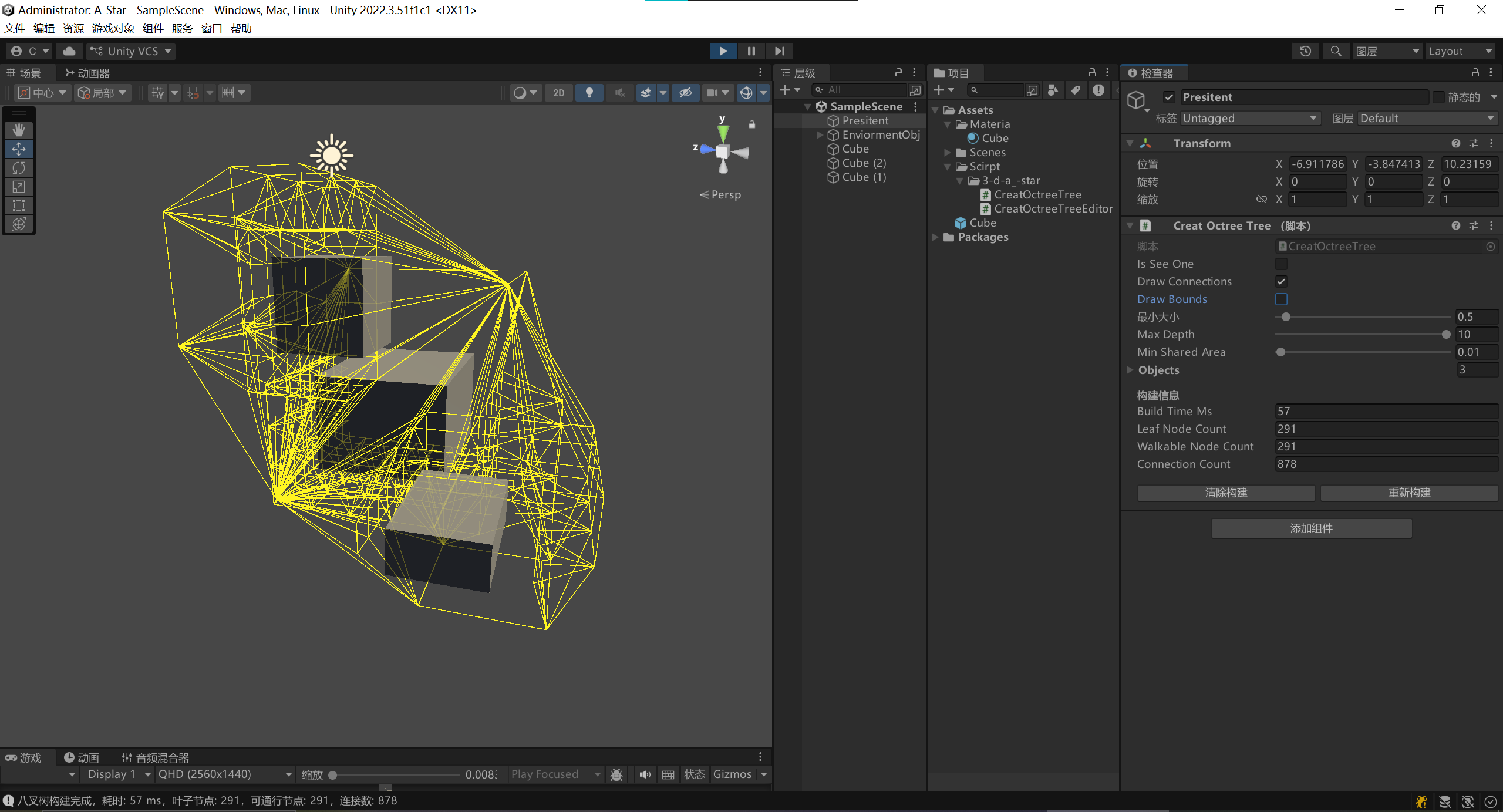
开始寻路
接下来我们终于可以开始进行最关键的一步, A* 寻路
1. 算法流程
首先我们来了解一下什么是 A*算法
A* 是一种启发式搜索算法,它结合了两种策略:
Dijkstra算法:保证找到最短路径(但效率低)
贪心最佳优先搜索:效率高(但不保证最优)
A* 的精髓在于使用一个评估函数:
F(n) = G(n) + H(n)┌─────────────────────────────────────────────────────────────┐
│ A* 算法流程 │
├─────────────────────────────────────────────────────────────┤
│ │
│ 1. 初始化 │
│ ├── Open列表 = [起点] (待探索的节点) │
│ └── Closed列表 = [] (已探索的节点) │
│ │
│ 2. 循环 (当 Open列表 非空) │
│ │ │
│ ├── 从Open列表取出 F值最小 的节点 → current │
│ │ │
│ ├── 如果 current == 终点 → 回溯路径,结束! │
│ │ │
│ ├── 将 current 加入 Closed列表 │
│ │ │
│ └── 遍历 current 的每个邻居 neighbor: │
│ │ │
│ ├── 如果 neighbor 在 Closed列表 → 跳过 │
│ │ │
│ ├── 计算新的 G值 = current.G + 移动代价 │
│ │ │
│ └── 如果 新G值 < neighbor.G: │
│ ├── 更新 neighbor 的 G、H、F 值 │
│ ├── 设置 neighbor.parent = current │
│ └── 将 neighbor 加入 Open列表(如果不在的话) │
│ │
│ 3. Open列表为空 → 无法到达终点 │
│ │
└─────────────────────────────────────────────────────────────┘假设我们要从 S 走到 E:
起点 终点
↓ ↓
┌───┬───┬───┬───┬───┐
│ S │ │ │ │ E │
├───┼───┼───┼───┼───┤
│ │ ▓ │ ▓ │ ▓ │ │ ▓ = 障碍物
├───┼───┼───┼───┼───┤
│ │ │ │ │ │
└───┴───┴───┴───┴───┘第1步:初始化
Open列表: [S(F=8)] ← 起点S,估计到E的距离是8
Closed列表: []第2步:探索起点S的邻居
启发函数 H(n) 我使用欧几里得距离(直线距离),因为八叉树节点可以向任意方向移动。
┌───┬───┬───┬───┬───┐
│ S │ 1 │ │ │ E │ 数字 = 探索顺序
├───┼───┼───┼───┼───┤
│ 2 │ ▓ │ ▓ │ ▓ │ │
├───┼───┼───┼───┼───┤
│ │ │ │ │ │
└───┴───┴───┴───┴───┘
Open列表: [1(G=1,H=3,F=4), 2(G=1,H=4,F=5)]
Closed列表: [S]第3步:选F值最小的继续探索
┌───┬───┬───┬───┬───┐
│ S │ 1 │ 3 │ │ E │
├───┼───┼───┼───┼───┤
│ 2 │ ▓ │ ▓ │ ▓ │ │
├───┼───┼───┼───┼───┤
│ │ │ │ │ │
└───┴───┴───┴───┴───┘最终:找到路径
┌───┬───┬───┬───┬───┐
│ S │ ★ │ ★ │ ★ │ E │
├───┼───┼───┼───┼───┤ ★ = 最终路径
│ │ ▓ │ ▓ │ ▓ │ │
├───┼───┼───┼───┼───┤
│ │ │ │ │ │
└───┴───┴───┴───┴───┘2. 我的实现中的优化
Ⅰ. 二叉堆优先队列
传统做法是用列表存储Open节点,每次要遍历找最小F值:
// ❌ 低效做法 - O(n)
PathNode best = null;
foreach (var node in openList)
{
if (best == null || node.F < best.F)
best = node;
}我使用二叉堆(最小堆),自动保持最小F值在堆顶:
public void Clear()
{
heap.Clear();
indexMap.Clear();
}
public bool Contains(OctreeTreeNode node)
{
return indexMap.ContainsKey(node);
}
public void Enqueue(PathNode node)
{
heap.Add(node);
int index = heap.Count - 1;
indexMap[node.Node] = index;
BubbleUp(index);
}二叉堆的具体实现原理就不在此赘述,网上能搜到的教程很多
通俗来说就是实现一颗完全二叉树(除最后一层外,每一层都是满的最后一层的节点 从左到右依次排列),每次插入新元素都将其放在末尾,并于父节点比较,若小于父节点(升序二叉堆情况),就上浮(与父节点进行交换),反复比较直至大于等于父节点。
Ⅱ. HashSet 快速查询
// ✅ O(1) 查询
private HashSet<OctreeTreeNode> closedSet;
if (closedSet.Contains(neighborNode)) continue; // 极快!Ⅲ. 数据分离设计
private class PathNode
{
public OctreeTreeNode Node;
public PathNode Parent;
public float G; // 从起点到当前节点的实际代价
public float H; // 从当前节点到终点的启发式估计
public float F => G + H; // 总代价
public PathNode(OctreeTreeNode node)
{
Node = node;
Parent = null;
G = float.MaxValue;
H = 0;
}
}寻路数据与八叉树节点分离,好处:
不污染原始数据结构
支持多个寻路请求并发执行
3. 启发函数 H(n)
启发函数的选择直接影响算法效率:
private float Heuristic(OctreeTreeNode from, OctreeTreeNode to)
{
return Vector3.Distance(from.nodeCube.center, to.nodeCube.center);
}我使用欧几里得距离(直线距离),因为八叉树节点可以向任意方向移动。
启发函数的要求
4.路径平滑
原始路径会经过每个节点中心,看起来很生硬:
原始路径: S → ● → ● → ● → ● → E
↘ ↓ ↓ ↓ ↗路径平滑使用视线检测跳过不必要的中间点:
private List<Vector3> SmoothPath(List<Vector3> path)
{
if (path == null || path.Count <= 2) return path;
List<Vector3> smoothed = new List<Vector3> { path[0] };
int current = 0;
while (current < path.Count - 1)
{
int furthest = current + 1;
for (int i = path.Count - 1; i > current + 1; i--)
{
if (CanWalkDirect(path[current], path[i]))
{
furthest = i;
break;
}
}
smoothed.Add(path[furthest]);
current = furthest;
}
return smoothed;
}最后寻路效果

详细代码篇幅较长,可访问下面链接获取
文章部分图片及代码来自https://developer.unity.cn/projects/665be20eedbc2a001ec6413d

